Implement a Fully Homomorphic Version of the AES-128 Cryptosystem using TFHE-rs

In homomorphic encryption, transciphering is the concept of applying an encryption or decryption algorithm homomorphically. This was the subject of the TFHE-rs Bounty Season 7, where hunters were asked to homomorphically apply the AES encryption algorithm. 

In practice, transciphering can reduce the size of encrypted data for storage or transmission. For example, since FHE encryption can significantly increase message size, a practical strategy to limit the amount of exchanged data is to send the AES encryption of the message alongside the FHE encryption of the AES key. Then, by applying the decryption homomorphically, the overall communication overhead can be reduced.

We received many very high quality submissions, and choosing a winner was particularly challenging. We were especially excited to see the variety of strategies implemented by the different submissions, each leveraging different parts of the TFHE-rs API in unique ways.

After careful review and benchmarking, we awarded the grand prize to the submission from "sharkbot".

The challenge

For this bounty, we were interested in the "counter" mode of encryption for AES (Figure 1). In this mode, the plaintext is divided into 128-bit blocks. The AES cipher encrypts a counter consisting of a 64-bit randomly chosen nonce (IV) and a 64-bit incremental value for each block. Each block of plaintext is then XORed with the output of the AES cipher.

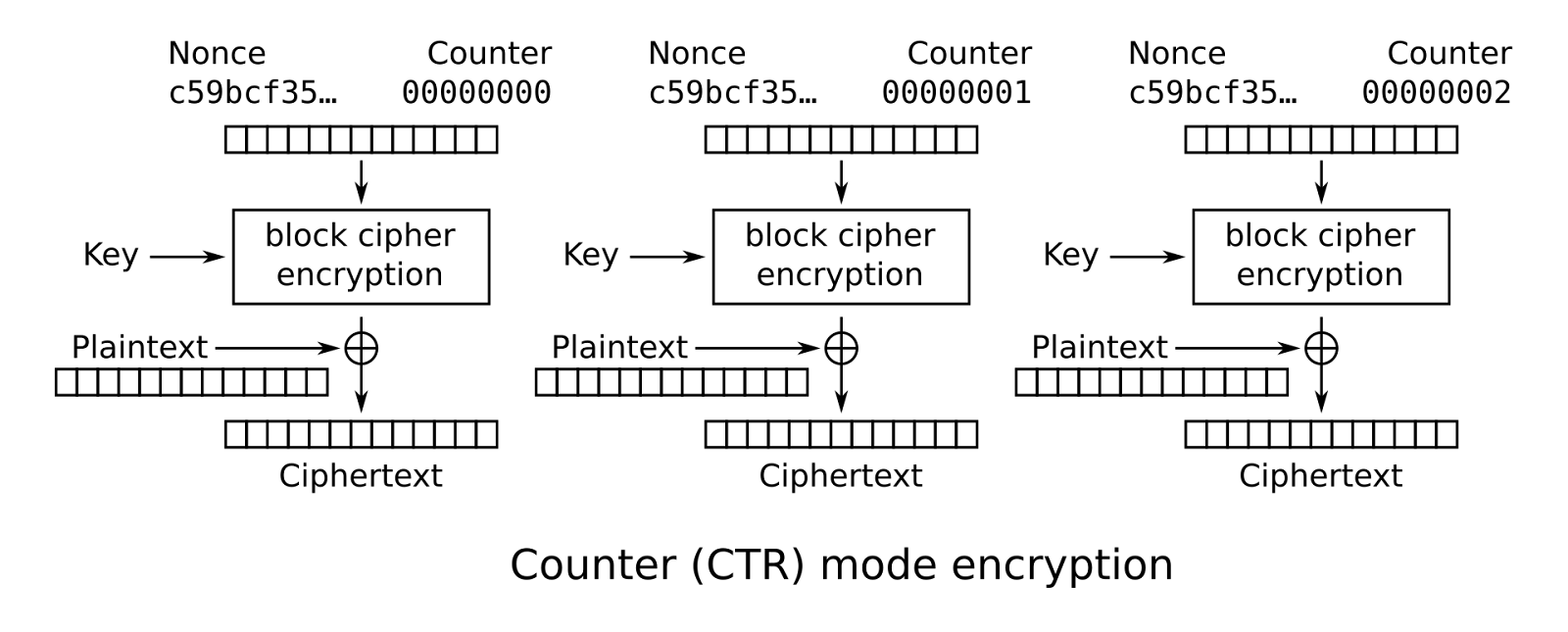
This type of encryption mode is particularly suitable for FHE because it can be easily parallelized.

The AES block cipher is first initialized with the KeyExpansion process, which expands the initial 128-bit key into 11 round keys—one for initialization and 10 for the encryption rounds.

The [.c-inline-code]KeyExpansion[.c-inline-code] itself consists of several steps, notably including multiple applications of the [.c-inline-code]SubBytes[.c-inline-code] operation, which is explained further below. 

Then, each 128-bit block of plaintext undergoes a loop of 10 rounds. Each round applies the following steps: [.c-inline-code]AddRoundKey[.c-inline-code], [.c-inline-code]SubBytes[.c-inline-code], [.c-inline-code]ShiftRows[.c-inline-code], and [.c-inline-code]MixColumns[.c-inline-code].

• AddRoundKey: A simple XOR between the round key and the current state.
• ShiftRows: Byte-wise shifting in the state—essentially free under FHE computation.
• MixColumns: More complex, requiring XORs and multiplications within a Galois field.
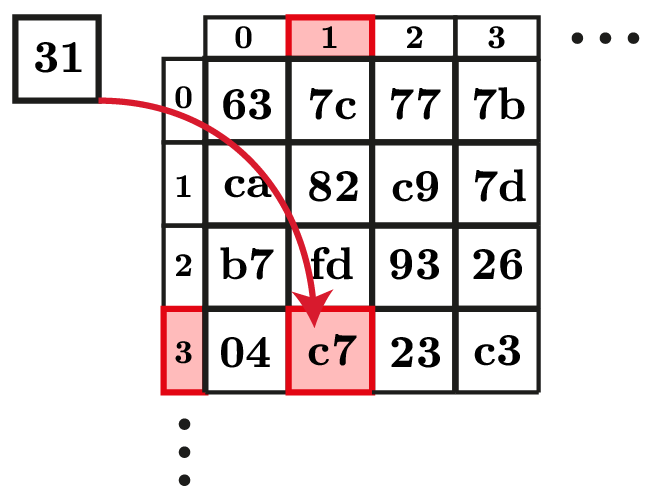
• SubBytes: Applies a non-linear lookup table (the S-box) to each byte (Figure 2). This step is essential for AES security and presents the biggest challenge for FHE implementation.

‍

As explained in the TFHE-rs Deep Dive series, one of TFHE-rs' key features is the bootstrap operation, which enables the application of look-up tables (LUTs). However, the challenge in the Bounty Program Season 7 was that the AES S-box is too large to fit into a single TFHE LUT with most optimized parameter sets. Handling this constraint was the main differentiator among the submissions we received.

The winning solution

Sharkbot's submission stood out by treating the S-box as a computable bit-level circuit rather than a byte-level LUT. This kind of approach is not specific to FHE, and has been explored for AES implementations running in low-power electronic devices. 

Specifically, sharkbot implemented an FHE version of the Boyar-Peralta circuit for the AES s-box. This compact circuit supports both forward and reverse S-box computations, making it reusable for decryption as well. It consists of a series of XOR and AND operations over input bits. 

To perform these operations, the winning submission implemented the following strategies:

• Shortint layer: Used the low-level shortint API of TFHE-rs to directly manipulate encrypted bits.
• Parameter tuning: Selected parameters carefully to maximize linear (cheap) operations and limit the use of expensive bootstrapping to when noise refresh was necessary.
• Parallelism: Parallelized operations inside each AES block and across different AES blocks. Analyzed the data dependency graph of the S-box computation to enable safe and effective parallel execution.

As a result, the submission achieved optimal utilization of the CPU cores of our benchmark machines, making it the most efficient solution we received.

These techniques enabled the AES encryption algorithm to be executed fully under FHE, as shown below:

	let encrypted_round_keys = fhe_key_expansion(&sks, &mut encrypted_key);

	let mut encrypted_counters = fhe_generate_counters(&sks, number_of_outputs, &encrypted_iv);

	encrypted_counters.chunks_mut(thread_pools.len()).for_each(|chunk|{
    	  chunk.par_iter_mut().enumerate().for_each(|(i, input)|{
        	thread_pools[i % thread_pools.len()].install(||{
            	fhe_aes_encrypt(&sks, input, &encrypted_round_keys);
        	});
    	  });
	});

(Note: This implementation has not yet been integrated inside TFHE-rs.)

Other notable submissions

A very similar approach was taken by "tomtau", who took second place. Their s-box implementation also used a Boyar-Peralta circuit, but this time was inspired by the work of Nigel Smart, who has designed similar circuits for use in an MPC context. The implementation is done using the boolean API of TFHE-rs.

Benchmark results ultimately determined the final ranking:

• 🥇sharkbot: ~1 FHE AES encryption every 2 seconds (after a 14-second KeyExpansion)
• 🥈tomtau: ~1 FHE AES encryption every 6 seconds (after a 6-second KeyExpansion)
• 🥉allanbrodum : ~1 FHE AES encryption every 3 seconds, but with a 34-second KeyExpansion.
  (Note: Allanbrodum’s submission performed IV incrementation in the clear, so it was not fully homomorphic.)
  

All benchmarks were run on an [.c-inline-code]AWS hpc7a.96xlarge[.c-inline-code] instance with 192 physical CPU cores.

Conclusion

This bounty season highlighted how hardware design techniques—such as efficient bitwise circuits—can significantly improve FHE computations. This principle already appears in parts of TFHE-rs (for example, our shift/rotate operations use a barrel shifter), and it remains a promising area for optimization.

It also showcased the flexibility of the TFHE-rs API. While the newly stabilized high-level API covers most generic integer operations efficiently, lower-level access can still unlock additional performance for specific use cases like the AES S-box.

Congratulations again to all winners. See you at Season 8!

Additional links

• Star Zama's TFHE-rs GitHub repository to endorse our work.
• Review Zama's TFHE-rs documentation.
• Get support on our community channels.
• Participate in the Zama Bounty Program to get rewards in cash.

‍