The Game of Life : Rebooted

In July 2022, Zama announced the latest release of the Concrete Framework that aims at simplifying the use of Fully Homomorphic Encryption, or FHE, a powerful tool allowing users to compute over encrypted data. The goal of this blogpost is to see this new version of Concrete in action. We will upgrade an already existing example, Conway’s Game of life by Optalysys, using concrete-boolean so it can benefit from new features available in Concrete v0.2.

The Game of Life

The Game of Life is composed of a board (6x6 in this example) of cells. Each cell is either dead or alive. Each cell status is updated iteratively round by round, following this set of rules:

1. Birth: A dead cell with three (no more, no less) alive neighbors becomes alive on the next iteration.

2. Survival: An alive cell with two or three alive neighbors stays alive on the next iteration.

3. Death: An alive cell with less than two or more than three alive neighbors dies on the next iteration.

A full introduction on Conway’s Game of Life is available in our previous blogpost. 

Concrete

The Concrete Framework includes a set of Rust crates. The front-end, Concrete, is based on several crates containing cryptographic implementation of operators dedicated to specific message types. Namely, there is Concrete Boolean, which allows homomorphic computation of Boolean gates over ciphertexts, encrypting either true or false. The concrete-shortint crate contains operations for integers whose size does not exceed 7 bits. Finally, the concrete-integer crate allows the user to work with larger integers, offering 16 bits of precision. Each crate depends on the concrete-core crate, containing low-level cryptographic primitives. 

Concrete encompasses all the previous types with an easy-to-use interface, offering syntax as close as possible to that used by Rust : homomorphic operations are, when possible, associated with the same symbol or their clear equivalent. For instance, the computation of an ‘AND’ gate is simply done with the symbol ‘&’ between two ciphertexts, an addition is performed using a ‘+’, etc. In the end, ‘homomorphizing’ a program, i.e., adapting the source code to work on encrypted messages instead of clear ones, is really easy using Concrete.

Similarly, transforming an existing program written with concrete-boolean to concrete is not difficult and makes source code easier to read. This process is detailed in what follows. 

‍

Migrating from concrete-boolean to concrete using homomorphic Booleans

The starting point is the Optalysys implementation of the Game of Life based on concrete- boolean. The goal is to make explicit the modifications required to obtain the same program based on concrete. In order to match real life use cases, the overall process is divided into two parts: one dedicated to client computations and the other to the server. 

Client side

The first step when using concrete consists in defining the configuration. In this case, the targeted homomorphic type is the Boolean. Then, in the configuration builder, all other homomorphic types are disabled but the Booleans:

let config = ConfigBuilder::all_disabled().enable_default_bool().build();

Second, the configuration is used to generate the keys accordingly:

let (client_key, server_key) = generate_keys(config);

The client key must be kept secret and protected because this key allows the client not only  to encrypt but also to decrypt data! The server key is meant to be shared with the server in order to let it compute over the encrypted data. The last step is now to encrypt the input data:

let a = FheBool::encrypt(true, &client_key);

The last step for the client is to send the encrypted data along with the server key. 

Server side

On the server side, the context is set using the server_key, thanks to the following function:

set_server_key(server_key);

At this point, the only remaining work is to translate operations using common Rust symbols. In this example, the XOR gate in concrete-boolean, denoted by server_key.xor(a, &b) becomes a^b in Concrete. In the same manner, the AND gate is updated. The complete piece of code dedicated to the addition computation of the neighbors cell states, also called the accumulator sum, is exposed below. 

Here is the old code with concrete-boolean:

let c1 = server_key.xor(a, &b.0);
let r = server_key.and(a, &b.0);

let c2 = server_key.xor(&r, &b.1);
let r = server_key.and(&r, &b.1);

let c3 = server_key.xor(&r, &b.2);

Here is the new code with concrete:

let c1 = &self.0 ^ rhs;
let first_carry = rhs & &self.0;

let c2 = &self.1 ^ first_carry;
let second_carry = &first_carry & &self.1;

self.2 = &self.2 ^ second_carry;

The second example is about the application of the previous function to the computation of the new cell state. It contains new operations, like the NOT and OR gates, but also combinations of operations.

Here is the old code with concrete-boolean:

// perform the sum
let sum_neighbours = sum(server_key, neighbours, zeros.clone());

// check if the sum is equal to 2 or 3
let sum_is_2_or_3 = server_key.and(&sum_neighbours.1, &server_key.not(&sum_neighbours.2));

// check if the sum is 3
let sum_is_3 = server_key.and(
		&sum_neighbours.0,
		&server_key.and(&sum_neighbours.1, &server_key.not(&sum_neighbours.2)),);

// return (an encryption of) the new state of the cell
server_key.org(&sum_is_3, &server_key.and(cell, &sum_is_2_or_3))

Here is the new code with concrete:

// check if the sum is equal to 2 or 3
let sum_is_2_or_3 =!accumulator.2 & accumulator.1;

// check if the sum is 3
let sum_is_3 = &sum_is_2_or_3 & accumulator.0;

// return (an encryption of) the new state of the cell
sum_is_3 | cell & sum_is_2_or_3

The upgraded code is much simpler: the combination of functions is as easy to read as common Rust conditional statements. Notice that since the server key does not appear in any code lines referring to homomorphic operations, the concrete version of the program looks exactly like a program computing over clear data.

Migrating from Concrete homomorphic Boolean to Concrete homomorphic integers

In the case of the Game of Life, using the Boolean type to represent a cell state is natural since there are only two possibilities (dead or alive). However, the computations of the accumulator containing the state of the neighbor cells then requires some tricks. In a nutshell, one cell is surrounded by eight others, and its new state depends on the value of the sum of each neighbor state. As seen before, the current approach uses three homomorphic booleans, where a sum function is redefined to simulate an addition over three bits. Employing homomorphic integers over three bits seems to be a more instinctive approach.

In Concrete, numerous types are proposed to work with homomorphic unsigned modular integers. The type nomenclature FheUint followed by a number X (e.g., FheUint3), represents ciphertexts encrypting integer messages over X bits. Each of these types embeds a carry buffer of the same size as the message. In the example of FheUint3, this means that the carry buffer size is equal to three bits. Having a space dedicated to carries is useful, among other reasons, to enlarge the number of homomorphic operations available, like computing any functions over two ciphertexts.

If the most trivial approach to translate the accumulator addition is to use FheUint3,  knowing that FheUint2 can contain four bits of information (two bits for the message and two for the carry) gives the possibility to optimize performance. In particular, the accumulator sum can be computed exactly using the four bits. In the Game of Life, only the first two bits contain useful information (i.e., the sum is equal to 2 or 3). This means that the accumulator can be computed using FheUint2. Thus, using homomorphic types encoding smaller messages leads to better performance. 

The objective of this section is to detail the steps required to convert a program written with FheBool to another using FheUint, using the Game of Life as an example. The overall process is really close to the previous one: updating the configuration builder, changing the types from FheBool to FheUint, and rewriting the accumulator addition.

Client side

The only type required is now FheUint2. The configuration is then given by:

let config = ConfigBuilder::all_disabled().enable_default_uint2().build();

The encryption function slightly changes to become:

FheUint2::try_encrypt(x, &client_key).unwrap())

To mimic the usual Rust behavior, the encryption function is prefixed by ‘try’. This will return an error in the case where the input message cannot be encoded over the number of bits of the FheUint. For example, trying to encrypt the message “10” over an FheUint2 will return an error, since “10” is encoded over three bits.

Server side

The accumulator sum is completely rewritten: using FheUint, the operation is simply done by a homomorphic addition over neighboring cells. Therefore, the new code for the accumulator becomes: 

let mut num_neighbours_alive = FheUint2::try_encrypt_trivial(0).unwrap();
for n in neighbours {
		num_neighbours_alive += *n;
}
num_neighbours_alive.eq(3) | (cell & num_neighbours_alive.eq(2))

The comparisons are done using the ‘.eq()’ function. Note that the Rust language does not offer the possibility to overload the ‘==’ symbol for homomorphic types: it requires that the output of the operation returns a Bool type, whereas only encrypted values are returned in this case. This constraint is true for any comparison operations. However, bit-wise operations, like the ‘OR’ in this example, are realized using the ‘|’ symbol.

Remark: since the variable neighbours is of type &[&FheUint2], the sum of all values contained in the array can be computed as in Rust, using the ‘.sum()’, e.g.:

let num_neighbours_alive: FheUint2 = neighbours.into_iter().copied().sum();

Performance comparison

In what follows, the table shows the comparison between the execution timings obtained from the different homomorphic types used. The first row contains the timings in seconds to update the complete 6x6 board. The second one contains the size of the associated keys, both client and server. The machine specifications are: 11th Gen Intel(R) Core(TM) i5-11400H@2.70GHz, 32GB of RAM. Benchmarks are realized using the command:

‍

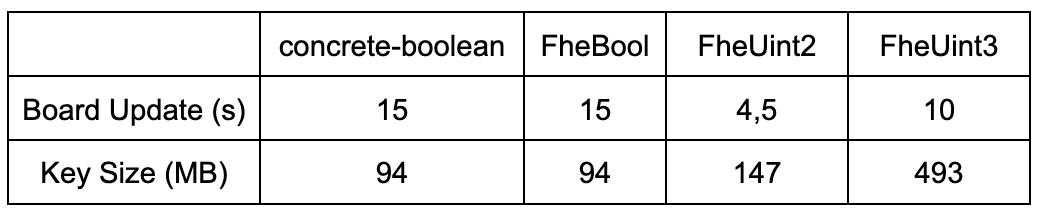
This shows that using the FheUint2 arithmetic instead of the Booleans improves performance by a factor of 3,3. Note that the key size is however larger (147MB vs 94MB).  

For the sake of completeness, comparison with other types has been added. First, there is no difference between using concrete-boolean or concrete. Second, even using a naive approach with FheUint3 already leads to a performance improvement of 33%. 

At the moment, all implementations are sequential. In a following blogpost, the process to parallelize will be described, so make sure to subscribe to Zama's newsletter to not miss it!

Additional links

- ⭐️ Star Concrete on Github, we're open-source.

- Documentation

- Subscribe to Zama's newsletter

- Follow Zama on twitter

‍

This blogpost was written by Jean-Baptiste Orfila with the help of Thomas Montaigu and Alexandre Quint.