Privacy-preserving insurance quotes

Last week we released Concrete Numpy, a python package that contains the tools data scientists need to compile various numpy functions into their Fully Homomorphic Encryption (FHE) equivalents.

Today, we will show you how to build an FHE-enabled insurance incident predictor. You can reproduce the results shown here by running the associated notebook in the Concrete Numpy documentation.

Let’s say you’re looking for a new car insurance policy and would like to compare some quotes. You can compare quotes online, but this requires you to fill in some personal information, such as your home address, date of birth, and driver license number. This data could be stored by the websites and your implicit permission is buried somewhere in a very long Terms of Service contract. You might be aware of data leaks where large databases of personal data were obtained by malicious parties using it for identity theft, so you’re quite hesitant to use such a service.

How can technology overcome this issue of trust? The answer is Fully Homomorphic Encryption (FHE), a technology that allows third parties to provide applications on your data without actually getting access to it, meaning the data stays encrypted during processing. Thus, the service processes your data without having access to it, and you receive the quote without giving away any of your information. At the end, you will be the only one who can read the quote by decrypting it, and the remote service can only store encrypted data that would be useless to an attacker.

‍

Building a simple insurance incident predictor

Let’s now peer through an application developer’s perspective: How can I use my insurance quote predictor model on encrypted data?

At Zama, we are developing Concrete Numpy to allow data scientists and developers to train or convert machine learning models into the FHE paradigm. Let’s look at an example for car insurance.

First, we’ll train a model based on some open data from OpenML, following a tutorial from the popular scikit-learn framework. This data set contains 670,000 examples giving the frequency of car accidents for drivers of various ages, past accident history, car type, car color, geographical region, and so on.

‍

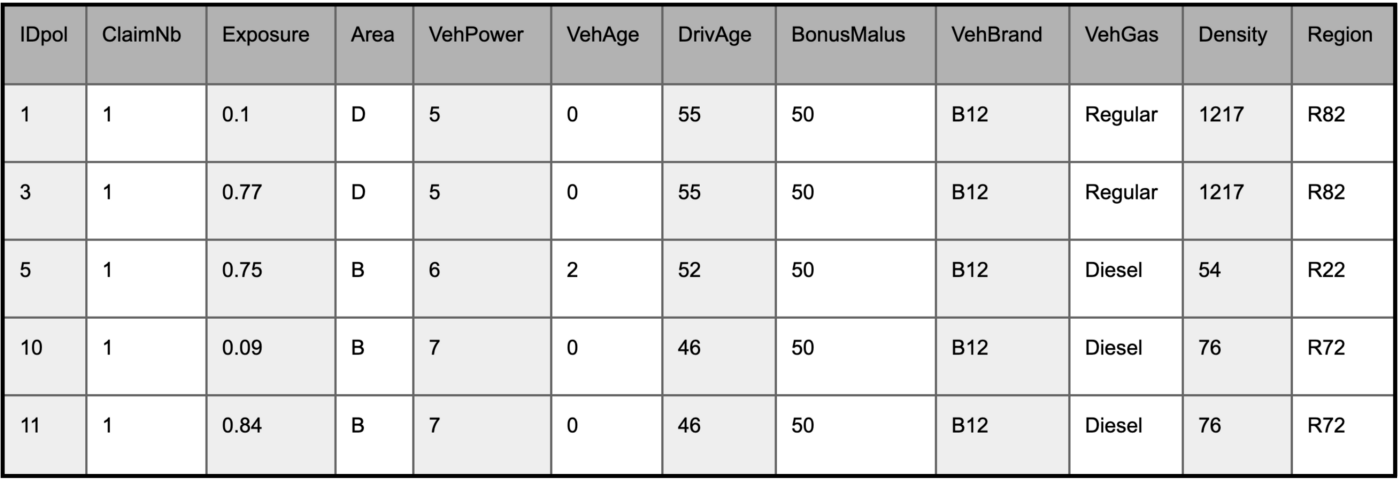
Some of the features are continuous, some ordinal, and some nominal. The target feature which is the frequency of car accidents (ClaimNb/Exposure), has a Poisson distribution.

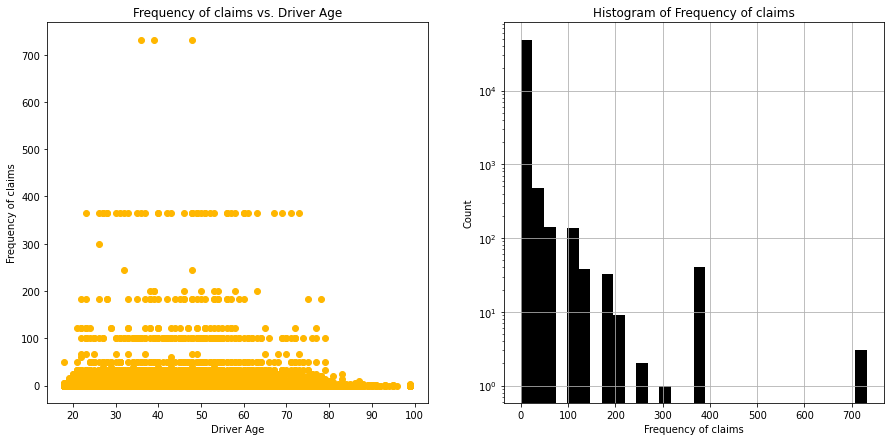
This suggests that if we are to model the frequency based on the other features we should use Poisson Regression. This technique is a generalized linear model with a log-link function:

Let’s first build a model with a single predictor variable, for which we can easily visualize the regression trend line. We will then build a full model with all the predictors. With scikit-learn, training a model only takes a line of code, and with a second line we will predict on the independent test set.

‍

Converting your model to FHE

So, how can you run this model in FHE? It’s simple if you use Concrete Numpy. We first need to quantize the model’s parameters to integers. In our implementation of FHE we cannot use floating point operations, but computations with floating points on integers can be pre-computed into lookup tables. These table lookups are executed with what is known as Programmable Bootstrapping (PBS), a unique FHE bootstrapping approach.

For Poisson regression, prediction requires to compute the linear part of the model w.x + b and then apply the inverse of the link function. In our case the link function is the natural logarithm so the inverse-link is the exponential function.

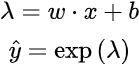
Using the Generalized Linear Model from Concrete Numpy, converting the model to FHE is easy, but requires a calibration set that converts the parameters w from floating point to integer and builds the PBS lookup table.

‍

Next, you compile the model to FHE with Concrete Numpy:

And you are ready to predict on encrypted test data:

‍
Let’s compare the results of the model in clear, working on floating point with the one compiled in FHE working with 5-bit quantized inputs and parameters:

‍

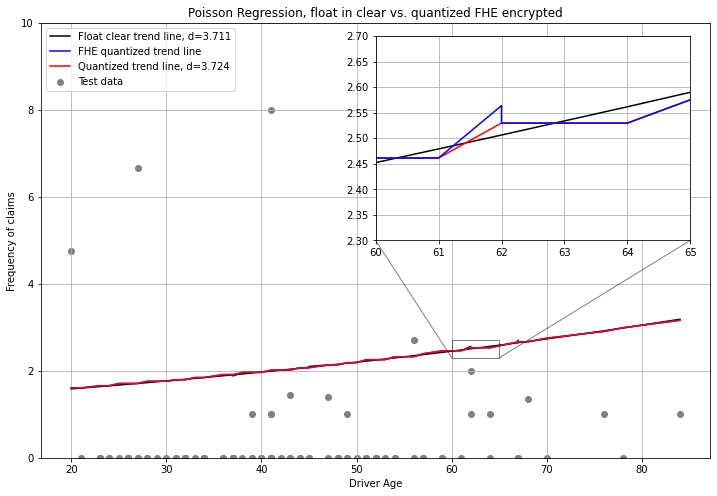
Analysis of the univariate model

It appears that this univariate model based on age is not a good predictor. The Poisson deviance which measures the goodness of fit is quite high. We do note that there is a slight degradation in the Poisson deviance (let’s call it d in the following) with the quantized FHE model. This is due to the fact that we quantized the inputs and the weights to 5 bits. We also note some noise in the FHE quantized model which is caused by the encryption scheme.

‍

Building a more complex model

Following the scikit-learn tutorial, we will now build a more complex model that uses all the predictor features. We proceed by transforming the raw features into ones that can be input to a regression model. Thus, the categorical features are transformed into one-hot encoding, and we also bin vehicle and person age. Transforming the data this way, we end up with a total of 57 continuous features (instead of the initial 11).

Here is where we encounter one of the limitations of our framework. We perform a dot product in the prediction, w . x, but in our framework the maximum integer size is, for now, limited to 7 bits. As every multiplication doubles the number of bits of precision of the inputs performing 57 multiplication-additions of integers to compute w.x would quickly overflow 7 bits.

We can compute the number of accumulator bits necessary for a certain number of dimensions of w and x when they are represented in b bits as :

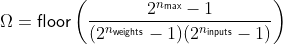
With 2 bits for the values in w and b, to keep the accumulator at 7 bits, we can afford up to 14 dimensions. Luckily we have tools, such as Principal Component Analysis (PCA), to reduce data dimensionality while minimizing the loss of information.

Let’s first perform a PCA to reduce dimensionality from 57 to 14 dimensions, and normalize the transformed features to have zero-mean. We create a scikit-learn pipeline to transform the features, do PCA, then fit the GLM:

Performing PCA in this case very slightly reduces our model’s predictive power:

Now let’s examine the effects of quantization and FHE compilation on the model. Note that when running the compiled FHE program, the results are identical to those of the quantized model in the clear, our FHE compiler does not introduce any loss of precision, thanks to the exact approach we have taken! We’ll now make a graph of the Poisson deviance for multiple quantization bit-widths.

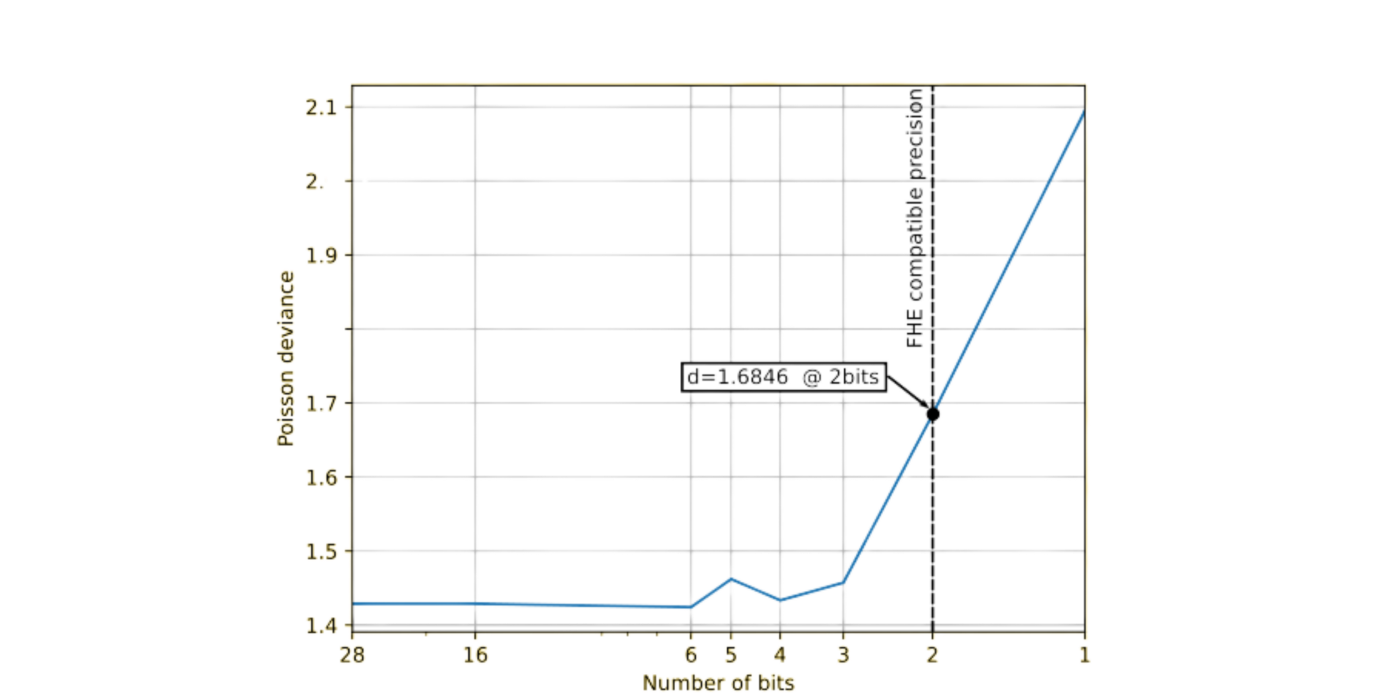
You’ll notice in this graph that the quality of the prediction (high deviance) starts getting worse around 3–4 bits. With 14 features we are forced to work in 2 bits. This will improve soon when we improve quantization tools in Concrete Numpy.

We can now complete the comparison:

‍

Conclusion

In this article, we looked at how you can use Concrete Numpy to convert a scikit-learn-based Poisson regression model to FHE. We have shown that, with the proper choice of pipeline and parameters, we can do the conversion with little loss of precision. This decrease in the quality of prediction is due to quantization of model weights and input data, and some minor noise can appear due to FHE.

All the results of this article can be produced by running the associated python notebook.

Thank you to Andrei Stoian for his contribution to this article.

Get the latest news about homomorphic encryption and what we do at Zama: subscribe to our newsletter.

We are hiring! Join Zama and help us safeguard privacy by making the internet encrypted end-to-end. All the info here: jobs.zama.ai

We’re open source — follow Zama on Github here: github.com/zama-ai