Onchain Blind Auctions Using Homomorphic Encryption and the fhEVM

This example uses an encrypted ERC20 token, which was introduced in a previous article.

‍

Blind auctions are notoriously hard to do in smart contracts, since all the transaction and states are public. While some solutions have been published, they either require using ZK and thus keeping the data off-chain, or using a 2 step process that includes a reveal function. Thanks to homomorphic encryption and the fhEVM however, it is now possible to run blind auctions fully on-chain, without the need for a reveal function.

The blind auction protocol we will be implementing here has two phases: a bidding and a claim phase. The bidding phase consists of users bidding an encrypted amount of tokens (using the encrypted ERC20 contract).

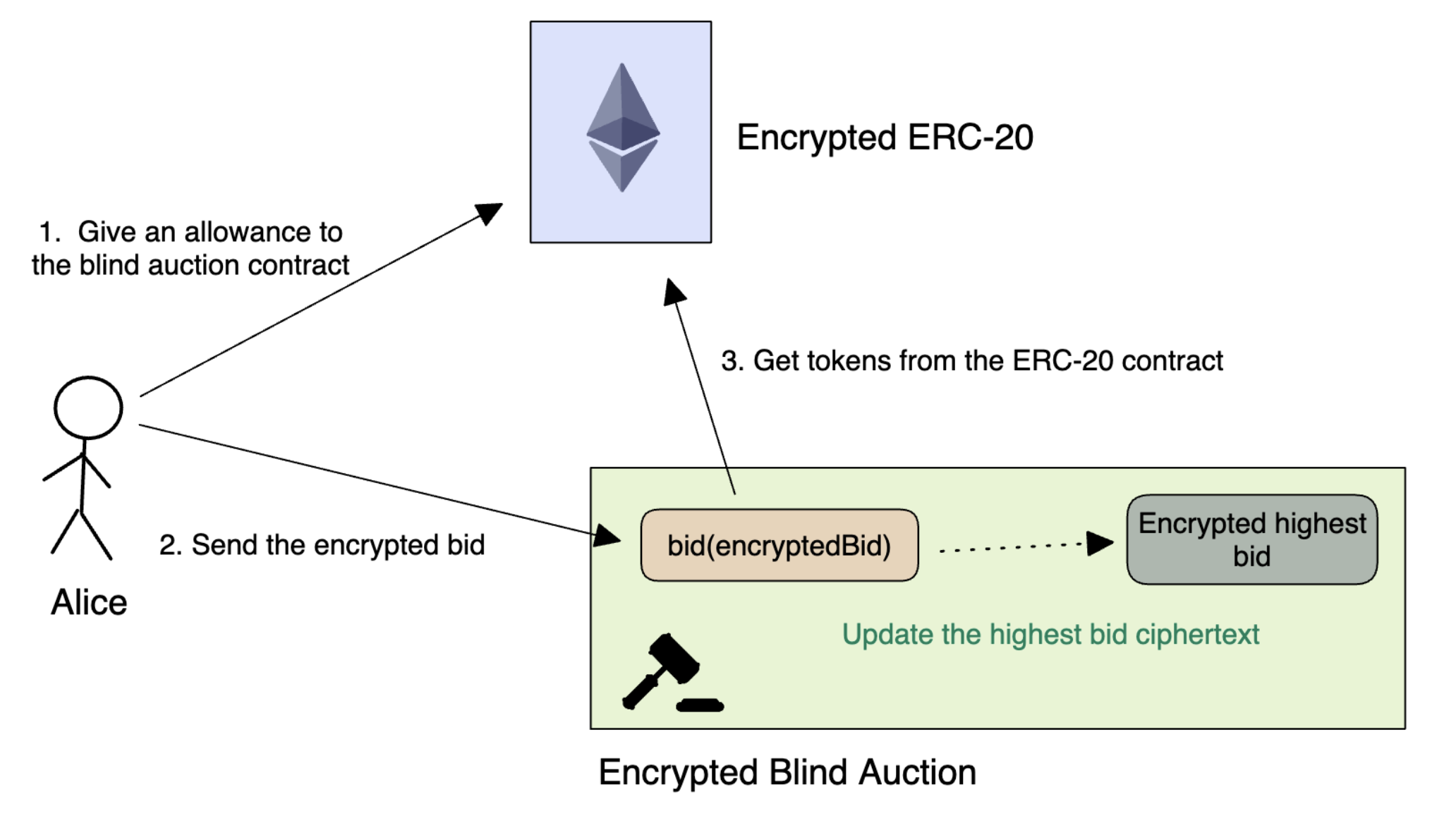
When the auction ends, the contract homomorphically determines who the highest bidder is. If the user is the highest bidder, they can claim their prize. If the user is not the highest bidder, they can withdraw their bidding tokens.

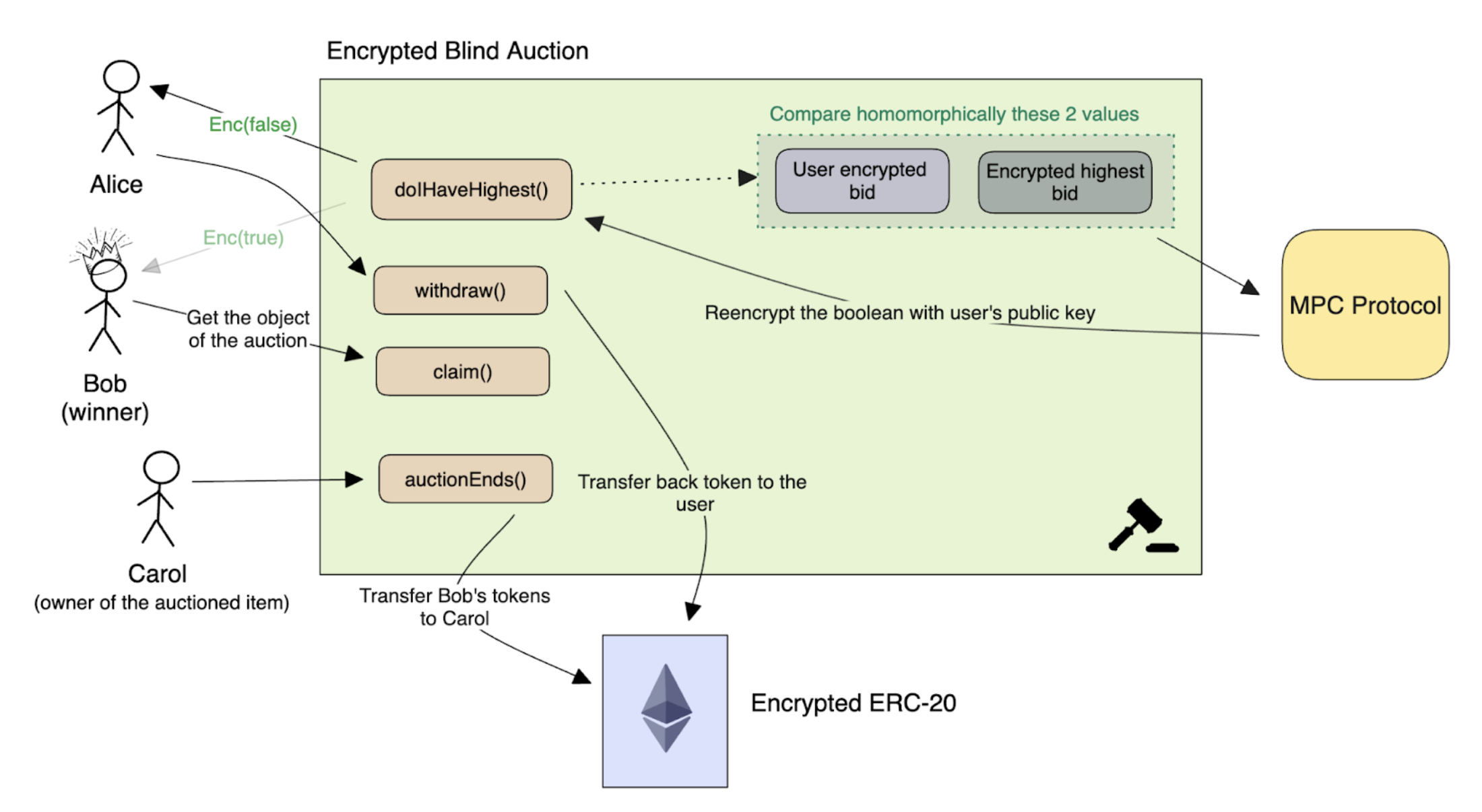
In the end, the contract only discloses the winning bidder, while keeping the winning bid value and non-winning bid values private.

‍

Writing our blind auction contract

The contract we will implement is almost identical to this non-encrypted one. We simply use the FHE data types where necessary to keep things hidden.

The first step in writing the blind auction smart contract is to define the auction parameters. This includes the address of the beneficiary, the encrypted ERC20 address, and the end time of the auction. These parameters are defined as properties in the smart contract code. Note that in the code below, the [.c-inline-code]euint[.c-inline-code] data type is used to represent encrypted unsigned integers.

import "../lib/TFHE.sol";
import "./EncryptedERC20.sol";

contract BlindAuction {
   // Timestamp where the auction ends
   uint public endTime;

   // Wallet address of the beneficiary
   address public beneficiary;

   // Current highest bid.
   euint32 internal highestBid;

   // Mapping from bidder to their encrypted bid value.
   mapping(address => euint32) public bids;

   // The token contract used for encrypted bids.
   EncryptedERC20 public tokenContract;

   // Whether the auction object has been claimed.
   bool public objectClaimed;

   // Whether the token has been transferred to the beneficiary
   bool public tokenTransferred;

   // The function has been called too early
   error TooEarly(uint time);

   // The function has been called too late
   error TooLate(uint time);

   // Event to dispatch when the object is claimed
   event Winner(address who);

   constructor(address _beneficiary, EncryptedERC20 _tokenContract, uint biddingTime) {
       beneficiary = _beneficiary;
       tokenContract = _tokenContract;
       endTime = block.timestamp + biddingTime;
       objectClaimed = false;
       tokenTransferred = false;
   }
}

‍

Writing the bid function

The bid function is split into two parts:

• When a user bids for the first time, we set the user’s bid to provided encrypted value
• If the user had placed a bid before, we check that the current bid is higher than the previous one, then transfer the difference between the new bid amount and the previous bid amount.

Once the bid is set, we compare the bid with the current highest bid for the auction. If the bid is higher, we update [.c-inline-code]highestBid[.c-inline-code]. 

But wait, how can we do an [.c-inline-code]if[.c-inline-code] statement on an encrypted value? Well, we can’t, which is why we need to modify the code to have the same effect, without using conditionals.

‍

Ifs without ifs

To illustrate how homomorphic conditionals can be implemented, let’s take a simple example, where user A wants to send tokens to user B. We need to check that user A has enough tokens without revealing any other data. This can be done with the following FHE code:

// TFHE.lte returns an encrypted 1 or an encrypted 0
hasEnoughToken = TFHE.lte(amount, balanceOfUserA);
_transfer(userB, amount * hasEnoughToken);

In this code, we first evaluate a homomorphic comparison checking that the user has more balance than the amount to be transferred. This homomorphic comparison will return an encryption of 0 if false, or an encryption of 1 if true. We then simply homomorphically multiply the amount by this encrypted comparison value, which will simply set the amount to 0 if the user doesn’t have enough balance. The transaction will still go through, and a new balance ciphertext will be generated, but it’s actual value won’t change (since we transferred 0 tokens).

Now applying this to the bid function, first when there is no existing bid:

function bid(bytes calldata encryptedValue) public onlyBeforeEnd() {
       // We verify the ciphertext
       euint32 value = TFHE.asEuint32(encryptedValue);
       euint32 existingBid = bids[msg.sender];
       // If there is no existing bid
       if (!TFHE.isInitialized(existingBid)) {
           // We set the current bid to the value
           bids[msg.sender] = value;
           // We transfer token from the user wallet to the smart contract address
           tokenContract.transferFrom(msg.sender, address(this), value);
       }

We can then check if the bid is the highest bid. If this is the first bid, it’s easy; otherwise, we need to perform a homomorphic comparison. The comparison is done with a method which acts as a ternary operator ([.c-inline-code]cmux[.c-inline-code] stands for encrypted mux, aka [.c-inline-code]condition ? value_if_true : value_if_false[.c-inline-code]) .

       euint32 currentBid = bids[msg.sender];
       if (!TFHE.isInitialized(highestBid)) {
           highestBid = currentBid;
       } else {
           // Returns encryption of 1 or 0 if current bid is higher than the previous highest bid.
           allTimeHigher = TFHE.lt(highestBid, currentBid)
           // Assign highestBid with current bid or highest bid
           highestBid = TFHE.cmux(allTimeHigher, currentBid, highestBid);
       }

It is important to keep in mind that each time we assign a value using [.c-inline-code]TFHE.cmux[.c-inline-code], the value changes, even if the plaintext value remains the same. 

Next, let’s implement the version where the user already has a bid, and wants to update it:

 function bid(bytes calldata encryptedValue) public onlyBeforeEnd() {
       ...
       if (!TFHE.isInitialized(existingBid)) {
           bids[msg.sender] = value;
           tokenContract.transferFrom(msg.sender, address(this), value);
       } else {
           // Is the new bid is higher than the previous one?
           euint32 isHigher = TFHE.lt(existingBid, value);
           // Update bid with correct value, depending of isHigher
           bids[msg.sender] = TFHE.cmux(isHigher, value, existingBid);
           // Transfer only the difference between existing and value
           euint32 toTransfer = value - existingBid;
           // Transfer toTransfer if the bid is higher using mul()
           tokenContract.transferFrom(msg.sender, address(this), isHigher * toTransfer);
       }
       ...
   }

‍

Going Once, Going Twice, Sold

Once the auction is over, participants will be able to claim their item, or get their tokens back:

• [.c-inline-code]auctionEnd()[.c-inline-code] transfers the correct amount of tokens to the beneficiary
• [.c-inline-code]claim()[.c-inline-code] allows the winner to claim their prize
• [.c-inline-code]withdraw()[.c-inline-code] allows other participants to withdraw their bid

To allow users to determine if they have the highest bid, we need to decrypt the encrypted boolean value expressing whether or not they have the highest bid. This is done via the [.c-inline-code]TFHE.reencrypt[.c-inline-code] method, which re-encrypts a ciphertext from the network’s public key under the user’s public key. This is done in Solidity with a simple view function. This view function however needs to be authenticated by having the user provide a signature in the contract method call so that the network knows the caller is actually the owner of the bid. The signed token respects the EIP-712 standard.

function doIHaveHighestBid(bytes32 publicKey, bytes calldata signature) public view onlyAfterEnd onlySignedPublicKey(publicKey, signature) returns (bytes memory) {
return TFHE.reencrypt(TFHE.lte(highestBid, bids[msg.sender]), publicKey);
}

With this method, the user can determine if they have the highest bid or not: if they do, the winner can use the [.c-inline-code]claim()[.c-inline-code] method, otherwise, they can withdraw their tokens.
The beneficiary can call [.c-inline-code]auctionEnd()[.c-inline-code] to start the transfer of tokens.

// Claim the object. Succeeds only if the caller has the highest bid.
function claim() public onlyAfterEnd() {
    require(!objectClaimed);
    require(TFHE.decrypt(TFHE.lte(highestBid, bids[msg.sender])));
    objectClaimed = true;
    bids[msg.sender] = TFHE.asEuint32(0);
    emit Winner(msg.sender);
}

// Withdraw a bid from the auction to the caller once the auction has stopped.
function withdraw() public onlyAfterEnd() {
    euint32 bidValue = bids[msg.sender];
    if (!objectClaimed) {
        require(TFHE.decrypt(TFHE.lt(bidValue, highestBid)));
    }
    tokenContract.transfer(msg.sender, bidValue);
    bids[msg.sender] = TFHE.asEuint32(0);
}
function auctionEnd() public onlyAfterEnd() {
    require(!tokenTransferred);
    tokenTransferred = true;
    tokenContract.transfer(beneficiary, highestBid);
}

‍

We have a winner

Using homomorphic encryption in a blind auction smart contract can provide an additional layer of security and privacy for participants. By following the steps outlined in this article, you can create a secure and transparent blind auction smart contract where bids are encrypted and computations are performed on the encrypted data. The claim function replaces the reveal function, allowing the winner of the auction to claim their prize without revealing the highest bid.

‍

Join the Zama x FHENIX hackathon during EthCC and take Zama's fhEVM for a spin!‍

Additional links

• Follow Zama on Twitter
• Check out Zama on Github
• Deep dive into Zama fhEVM smart contract protocol with this blog post

‍